12.2. Line-segment Intersections#
A line-segment can be described by its two endpoints, \(p_1\) and \(p_2\), and denoted by \(p_1p_2\). Note that the set of points on this segments can be expressed as \(p_1 + s(p_2-p_1)\) for a parameter value \(s\in[0,1]\).
To determine if \(p_1p_2\) intersects another line-segment \(q_1q_2\), we express the points on both segments in this way (with different parameters \(s,t\)), and set the points equal. This leads to the problem: Find \(s,t\in[0,1]\) s.t.
which can be reorganized as a 2-by-2 linear system of equations for \(s,t\):
If the line-segments are parallel, the matrix is singular. For simplicity we simply say that they do not intersect in this case, but a better implementation would determine if they actually overlap.
We implement the method in the function below, where we have also included a tolerance \(\delta\). This is useful to handle the case when the intersection is close to one of the endpoints, then \(\delta>0\) would allow for a small positive overlap and \(\delta<0\) a small negative overlap.
using LinearAlgebra
using PyPlot
function linesegment_intersect(p1, p2, q1, q2, δ)
A = [p2-p1 q1-q2]
b = q1-p1
if rank(A) == 2
st = A \ b
if all(-δ .≤ st .≤ 1 + δ)
pintersect = p1 + st[1] * (p2 - p1)
return true, pintersect
else
return false, nothing
end
else
# Warning: parallel lines, should check if they actually overlap
return false, nothing
end
end
linesegment_intersect (generic function with 1 method)
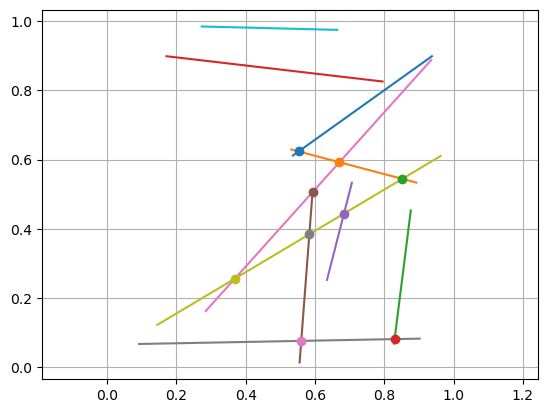
# Example: n random lines, find and plot all intersections
n = 10
lines = [ [rand(2), rand(2)] for i = 1:n ]
# Plot all lines
for line in lines
plot([line[1][1], line[2][1]], [line[1][2], line[2][2]])
end
# Find all intersections - note that we only consider j>i to avoid checking
# the same 2 line-segments twice
for i = 1:n
for j = i+1:n
isect, pq = linesegment_intersect(lines[i][1], lines[i][2], lines[j][1], lines[j][2], 0)
if isect
plot(pq[1], pq[2], "o")
end
end
end
axis("equal"); grid(true);