Procedural control flow
Mathematica also has procedural control flow (perhaps more familiar from e.g. Julia)

![]()
![]()
Which can be used for many if-else clauses

![]()
The simplest loop is the Do loop, which repeats the contents n times

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We also have traditional for loops

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
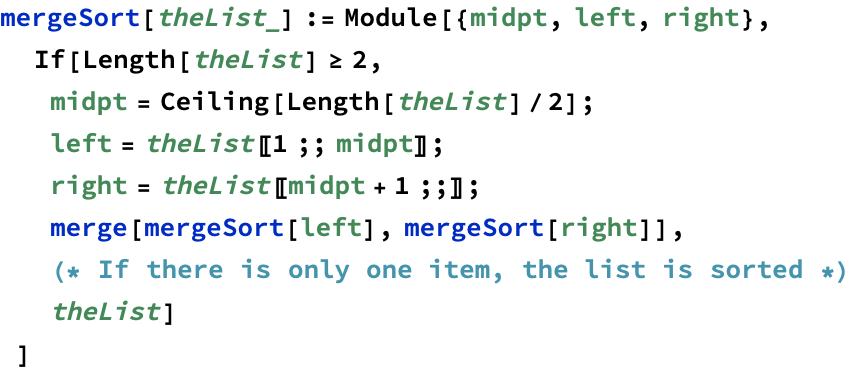
Application: merge sort
Merge sort is a recursive algorithm
Given a list, we:
1. find a midpoint
2. split the list at its midpoint into a left list and right list
3. sort the left and right lists using merge sort (recursion)
4. merge the two lists

![]()
![]()
![]()
![]()
The runtime complexity of merge sort is given by the recurrence
t(n)=2t(n/2)+O(n)
![]()
![]()
The runtime complexity is n log(n)
Functional-style merge sort

![]()
![]()
Finding all primes less than n
Algorithm known as the Sieve of Eratosthenes
Choose a number n
We will find all primes less than n
1. List all numbers 2 through n
2. Starting with, p=2, mark all multiples of p, beginning with ![]()
i.e. mark ![]() up to n
up to n
3. Repeat step 2 with p the next unmarked number
4. Terminate when ![]()

![]()
![]()
Let’s check our work...
![]()
![]()
We can also use a functional approach
![]()
![]()
![]()
