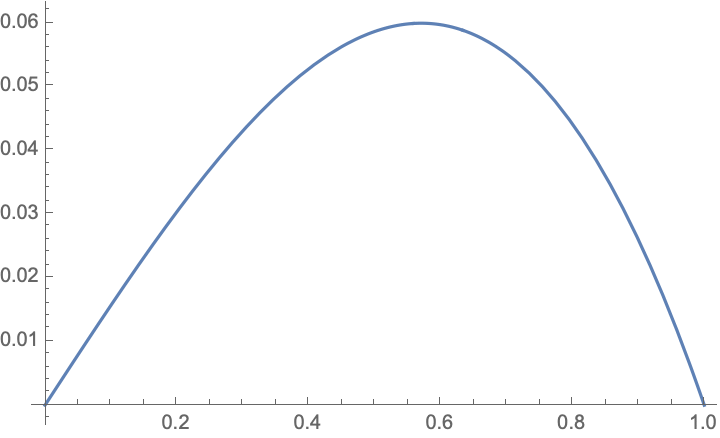
Using Mathematica for calculus
Mathematica is what Wolfram Alpha is based on (You may be familiar from Math 1A...)
There is very powerful built-in differentiation and integration of expressions:
![]()
![]()
Integrate can be used to compute indefinite integrals
![]()
![]()
Providing bounds of integration in the form of a list (just like in plotting) can be used to compute definite integrals
![]()
![]()
Numerical (approximate results) can be obtained using the N function
![]()
![]()
![]()
![]()
If we want to be fancy, we can use mathematical notation in our code:
![]()
![]()
![]()
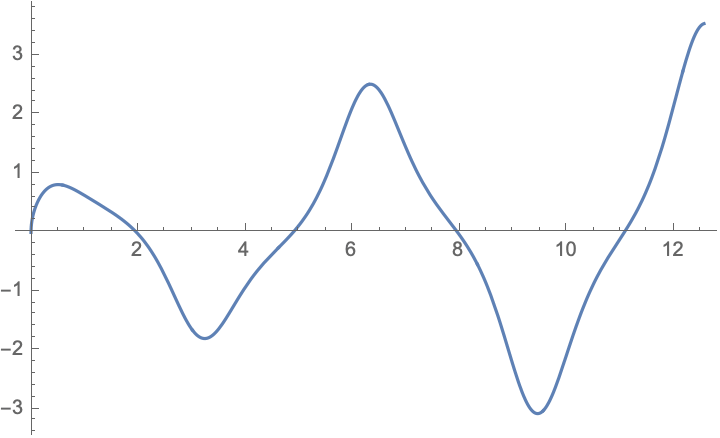
More calculus and series
Mathematica can easily compute partial and repeated derivatives
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finite and infinite sums can be computed using Sum
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Differential equations
Mathematica can find analytical solutions to many differential equations, both initial value problems and boundary value problems
The function DSolve looks for solutions to differential equations
![]()
![]()
We did not specify an initial condition, so the solution has a constant. Specifying the initial condition eliminates the constant
![]()
![]()
![]()
![]()
![]()
![]()
![]()
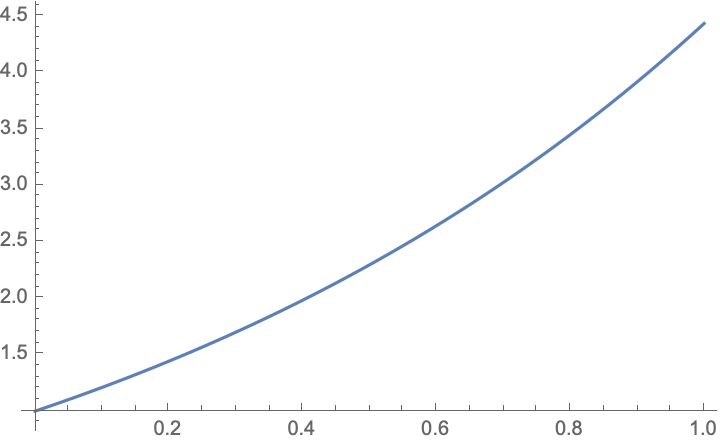
We can solve a boundary value problem:
![]()
![]()
![]()